Contrôle et géométrie : les mathématiques s'attaquent aux systèmes dynamiques
Créée en 2017, CAGE (pour Control And GEometry) est une équipe-projet commune Inria Paris/Sorbonne Université/CNRS, hébergée sur le campus de Jussieu au sein du Laboratoire Jacques-Louis Lions. Dirigée depuis ses débuts par Mario Sigalotti, directeur de recherche Inria, elle est constituée de six chercheurs permanents. Leurs travaux sont dédiés à différents aspects de la théorie du contrôle, une branche des mathématiques qui s’intéresse à l’évolution de systèmes dynamiques dont certains paramètres, appelés « contrôles », peuvent être modulés au cours du temps.
La théorie du contrôle est donc au cœur de nombreuses questions scientifiques ou problèmes concrets, comme le calcul de la trajectoire de vol d’une fusée, la simulation d’un réseau de distribution d’énergie, le choix de stratégies pour enrayer la propagation d’une épidémie, ou l’optimisation de la consommation d’une ressource, explique Mario Sigalotti. Au sein de l’équipe, nous travaillons ainsi sur des outils conceptuels et des méthodologies génériques en théorie du contrôle, que nous appliquons à trois thèmes scientifiques principaux : les modèles géométriques pour la vision, le contrôle des systèmes mécaniques quantiques et le contrôle des systèmes à dynamique incertaine.
Calcul et simulation dans les espaces non isotropes : la géométrie sous-riemannienne au cœur des travaux de CAGE
Parmi les outils théoriques auxquels s’intéresse CAGE, figure la « géométrie sous-riemannienne », un domaine de la géométrie qui peut trouver des applications dans de nombreux domaines scientifiques – typiquement en physique ou en biologie – ou techniques (comme l’automatique ou la robotique).
La géométrie permet de décrire de façon abstraite le monde qui nous entoure, par exemple afin de mesurer la dimension des objets, de suivre la trajectoire d’un avion ou de construire un ouvrage d’art. Celle de l’environnement que nous connaissons, avec ses trois dimensions (hauteur, largeur, profondeur), est dite « euclidienne » : les murs des bâtiments s’y rencontrent en angles droits, les voies ferrées le sillonnent en rails parallèles.
La géométrie « riemannienne », infiniment plus complexe, concerne des espaces courbes, ceux de surfaces alambiquées ou repliées, dans lesquelles toutes les notions de la géométrie euclidienne (comme les angles, les distances) prennent en un sens mathématique nouveau. La géométrie riemannienne vise, par exemple, à calculer les géodésiques, c’est-à-dire les chemins de longueur minimale, entre deux points d’une surface.
Quand garer sa voiture devient un exercice de géométrie sous-riemannienne
Et la géométrie sous-riemannienne ? Emmanuel Trélat, professeur de mathématiques à Sorbonne Université et chercheur de CAGE depuis sa création, explique l’objet des recherches de l’équipe : « Nous nous intéressons à des problèmes formulés dans le cadre riemannien et qui comportent de plus un certain nombre de contraintes. Imaginez-vous au volant de votre voiture : vous ne pouvez la déplacer qu’en marche avant ou arrière, les mouvements latéraux étant impossibles (ce sont les contraintes). Pour vous garer, vous devrez donc réaliser une combinaison complexe de mouvements, et parcourir une grande distance pour atteindre une configuration visuellement proche de la configuration d’origine (le plus court chemin entre deux points est une courbe complexe et non une ligne droite) : voilà le monde de la géométrie sous-riemannienne ! »
Décoder les secrets de la nature grâce à des concepts mathématiques
Parmi les domaines d’application de la géométrie sous-riemannienne, figurent la biologie et la médecine. C’est l’objet des travaux de Barbara Gris, docteure en mathématiques et titulaire de la bourse Emergence(s) attribuée par la ville de Paris, qui a rejoint le CNRS et l’équipe CAGE en 2019. Elle précise :
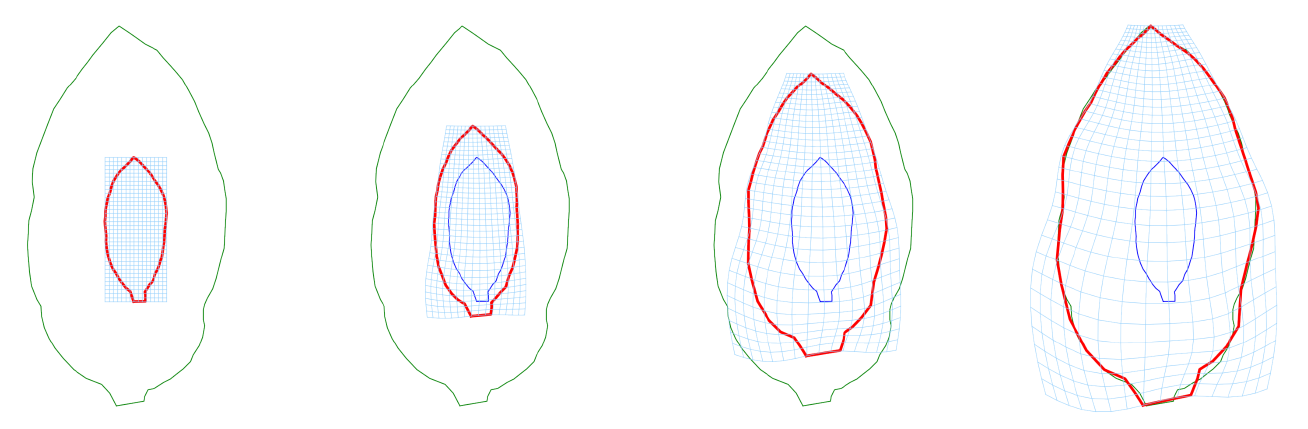
Mes recherches consistent à utiliser différents concepts mathématiques, comme la géométrie sous-riemannienne, pour découvrir les propriétés de certains processus complexes, comme la croissance d’organismes, ou la structure d’ensembles de données, comme celles issues de l’imagerie médicale.
Barbara Gris peut ainsi modéliser ces systèmes complexes, par exemple pour en prédire l’évolution ou en faciliter le traitement. À travers ses travaux théoriques, la mathématicienne contribue au développement d’outils numériques, dans le but par exemple d’aider à l’analyse des données d’IRM.
Les structures sous-riemanniennes se rencontrent aussi dans de nombreux champs scientifiques de pointe, notamment celui des innovations issues de la physique quantique qui se heurtent encore à des obstacles fondamentaux. « La manœuvrabilité de certains systèmes quantiques n’est pas facile à garantir et leur contrôle conditionne entre autres les performances de la métrologie quantique, explique Mario Sigalotti. La décohérence de ces systèmes s’accomplissant de façon extrêmement rapide, nous cherchons donc à étendre les outils de la théorie du contrôle pour décrire les actions qui peuvent être effectuées dans des temps très courts. »
Du quantique au spatial : les systèmes de contrôle se mettent au service de la science et de l'industrie
Cette voie de recherche, dans laquelle s’est engagée l’équipe, s’avère très prometteuse en raison de ses applications au calcul quantique, à la cryptographie quantique ou à la détection quantique (en particulier, l'imagerie par résonance magnétique nucléaire, très utilisée en médecine). Elle répond également à d’autres besoins, comme ceux de l’industrie aéronautique, spatiale ou de défense.
Emmanuel Trélat, qui a travaillé plus de dix ans au développement du dispositif de guidage de la fusée Ariane, souligne l’intérêt de ces recherches : « Développer des systèmes de contrôle en temps réel, avec les contraintes de l’informatique embarquée, comme les exigences de sécurité numérique et de sobriété énergétique, pose des problèmes théoriques complexes. Nos travaux contribuent à lever certains verrous technologiques et intéressent donc le monde industriel, avec qui nous engageons des projets de long terme. »
Pour mener à bien ses recherches de haut niveau, CAGE peut aussi compter sur le renfort de plus d’une dizaine de doctorants et postdoctorants. « Le dialogue avec d’autres scientifiques, en particulier avec des chercheurs ou des praticiens en médecine, apporte beaucoup à nos travaux. Les recherches doctorales constituent le moyen idéal de travailler avec des experts d’autres disciplines », estime Barbara Gris.
Des recherches utiles à divers secteurs économiques : quand les théories mathématiques offrent des solutions concrètes
Devant les multiples perspectives, l’équipe s’oriente déjà vers de nouvelles thématiques, soutenues notamment par Inria à travers le dispositif des actions exploratoires. « Nous souhaitons approfondir les questions de contrôle optimal, avec en ligne de mire des applications à la physique, par exemple pour améliorer le contrôle du confinement magnétique dans un réacteur de fusion nucléaire, ou encore l’efficacité de traitements médicamenteux », indique Mario Sigalotti.
S’ils aiment partager leurs résultats théoriques avec la communauté des mathématiciens, les chercheurs de CAGE cultivent aussi un vif intérêt pour les applications potentielles de leurs travaux.
Comme tout mathématicien, les recherches théoriques me passionnent et me motivent dans mon travail. J’apprécie cependant particulièrement la rencontre avec le monde des ingénieurs, qui doivent concevoir des objets répondant à un cahier des charges exigeant, car ces contraintes sont aussi sources de satisfaction, confie Emmanuel Trélat. Je l’éprouve en particulier quand une application industrielle réussie apporte une validation concrète à nos recherches. Je le vis alors comme un moment rare, qui me procure la sensation d’être utile à la société.
En savoir plus :
- Site de l’équipe CAGE
- Reconstruction d’images via le contrôle optimal par Hugo Boscain (vidéo), ENS, 15/06/2018.
- Tout est sous contrôle par Emmanuel Trélat (vidéo), Espace des sciences, 07/02/2012.