CMA-ES: optimization software for biology, medicine and engineering

55 million downloads. And 10,000 more each week. These are remarkable figures, especially for scientific software. “Yes, it's a lot. This is partly down to the explosion in artificial intelligence algorithms, which are now using our tool as an integrated library”, explains Anne Auger, head of RandOpt, the project team responsible for developing CMA-ES (Covariance Matrix Adaptation Evolution Strategy), building on research first started more than 25 years ago.

What exactly is this software used for? “It's used for optimising models. Let's say you are a biologist, for example, and you're studying the growth of bacteria. During your experiments you make measurements and you obtain data. At the same time, you also have a model made up of equations that the growth of the bacteria should obey. But this theoretical model has constants that are unknown to you. The issue here is that you will need to adjust these constants in order to match the experimental data that you have measured. That’s where CMA-ES comes in, enabling you to formulate this problem as an optimisation problem. CMA-ES will give you the correct constants, thereby minimising any existing errors between your theoretical model and the data you have measured. This is what is known as calibration. And calibration problems can be found everywhere, from biology and medicine to various fields within industry.” Hence why the software has proved so popular.

“CMA-ES is also widely used in science”, adds Nikolaus Hansen, the researcher behind the mathematical method employed by the software. “In geophysics, for instance, certain constants in some theoretical models are unknown, meaning that the parameters have to be calibrated in order to adapt models to the data. Otherwise they wouldn't be usable.”

It can also be used for image calibration.

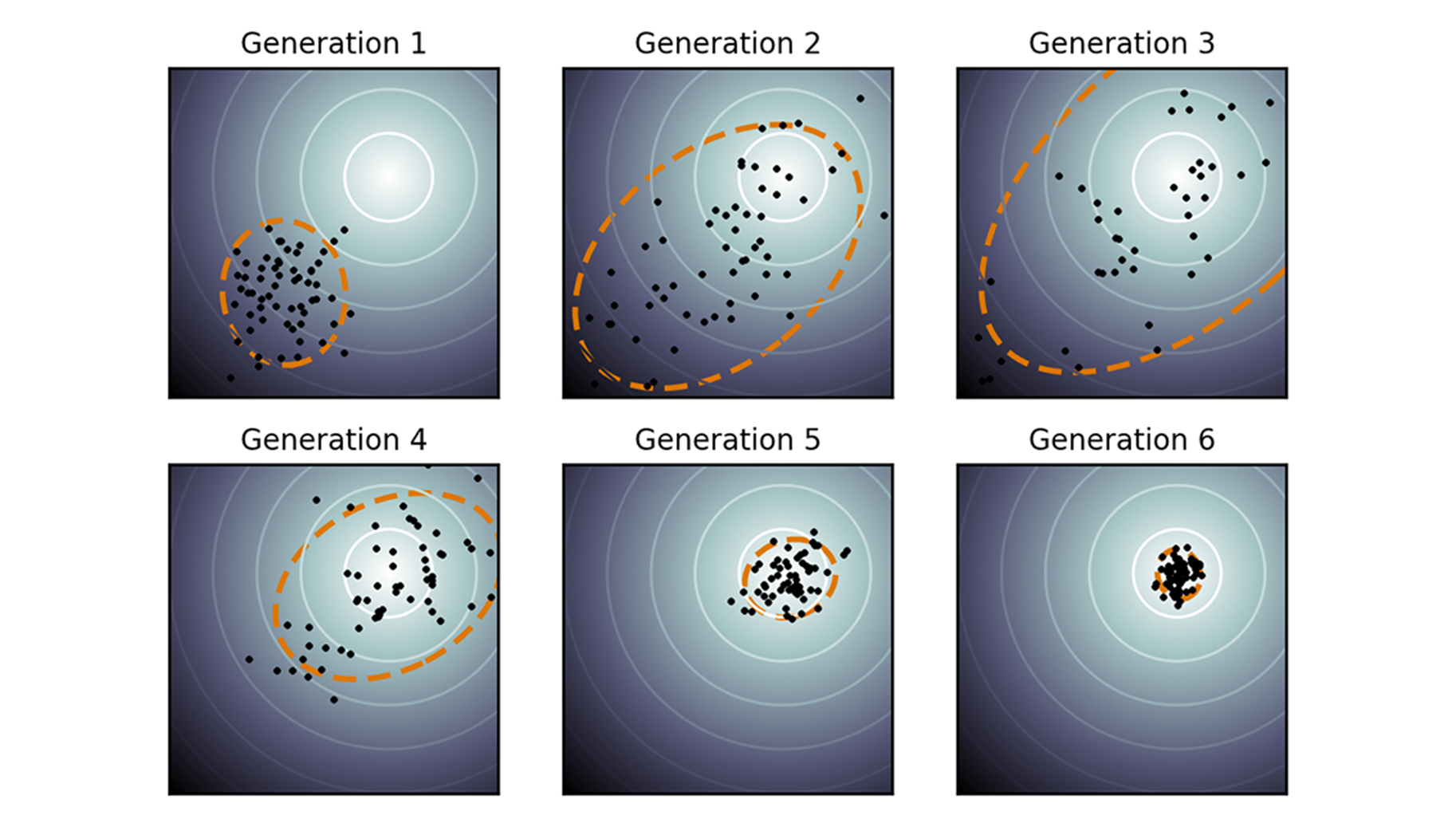
What sets CMA-ES apart is that it operates as a black box. “What this means is that the software doesn't need to know what the function it is tasked with optimising actually looks like”, explains Anne Auger. “It doesn’t need to access the equation for that function. Naturally it does interact with the function, but all it needs is to know whether or not the parameters are correct. Nothing else.”

CMA-ES operates as a black box. 

This has also attracted interest from manufacturers seeking to keep their intellectual property away from prying eyes. “We worked with the satellite manufacturer Astrium”, says Nikolaus Hansen. “They had an optimisation problem that they had been unable to solve for a long time, and they didn't give us much of a chance of solving it. They didn't want to share the source code that they had spent years developing, and only granted us access to an executable. But we were still successful with our optimisation, which really impressed them.”

At a basic level, the algorithm has no internal knowledge of the problem that it's optimising. “Let's use the example of a turbine blade. Finding the right performance level is a highly complex optimisation problem, generally a black box one. The manufacturer will carry out an air flow simulation. On our side of things, with CMA-ES, we don’t know what is going on within these simulations. In other words, we can’t predict the extent to which changes made to the shape of the blade will affect air flow. Different shapes are tried one after another, and this continues in order to make improvements. This is how the software works, through successive iterations.”

As a result, RandOpt has regularly found itself working with major industrial groups, particularly through the Cifre scheme, which involves companies funding PhDs. “We worked with Alstom, for example, using CMA-ES to improve flame control in a gas turbine. Again, this can be thought of as an optimisation problem.”

The team has also worked with Storengy, a subsidiary of the Engie group specialising in the underground storage of natural gas. “They were looking to model their reservoirs and they needed a model that adapted to the data gathered during core drilling. Another question concerned finding the ideal place to set up drilling points.”

Multi-objective optimization

“Some solutions might maximise one objective, but at the expense of other objectives. Either that or they have a negative impact on one objective in order to improve others.” says Anne Auger. The user is then able to make a decision, having been informed of all of the available possibilities.

“The PSA Group uses CMA-ES to optimise the design of cars”, explains Nikolaus Hansen. “These structures need to be as lightweight as possible, while also being as solid as possible, as aerodynamic as possible and as cheap as possible to manufacture. Some of these properties will inevitably contradict each other, and so optimisation doesn't come up with just one compromise, but rather a wide range of possible options. It is then up to the engineer to make their choice.”

Software inspired by biology

The mathematical method behind CMA-ES is very much in keeping with bioinspiration. “There’s this really fascinating idea that biological evolution works like an optimisation process and that the mechanisms observed in biology can also be used in technology”, says Nikolaus Hansen. 

For all that, it is worth noting that, “in 2019 we invited Nikolaus’s PhD supervisor to a conference”, says Anne Auger. “Despite how enormously successful CMA-ES had been, he confessed that he had never really liked the program.” Why? “He didn’t think it was sufficiently bio-inspired and felt it was too mathematical!”